mankiw ruleをjapanese dataで計算してみた

Krugumanがmankiw ruleについて書いている。

The Taylor Rule And The “Bond Bubble” (Wonkish)

一言でいうと、「長期金利が低下しているの見て債券バブルだという人がいるけど、mankiw ruleとかでも計算すれば長期金利低下は全然不思議じゃないということが分かるはずだよね」という感じの主張で、これを受けてMankiwも（他のいろいろあるversionのtaylor ruleではなく）、自分のルールに注目してもらってうれしいのか、反応している。

Krugman reestimates the Mankiw rule

そういえばtaylor ruleを自分でreplicateしたことがないので、これを機会にやってみる。まずは、KrugmanやMankiwのブログにある、アメリカでのmankiw ruleのreplicateをば。

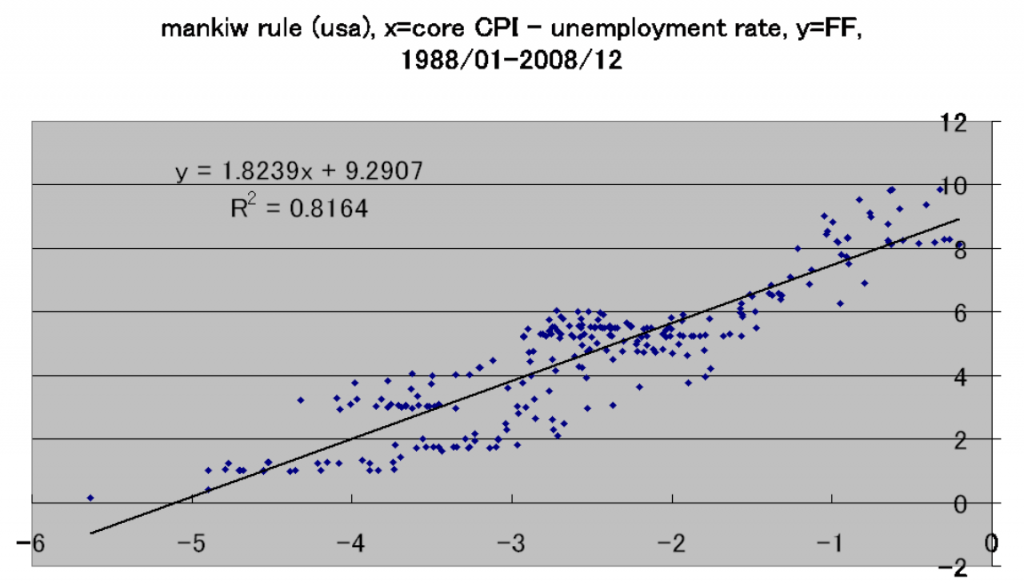
あれ。For some reasons, I can’t replicate completely Kruguman’s estimation. Data handlingでどこか間違えたか？ふむ・・・。まぁいいや、だいたい再現できた。で、現状アメリカではcore inflation=0.9% and unemployment rate=9.5%, which means x=-8.6, implying that FF should be -6.4! もちろんゼロ以下には出来ないが、これだけマイナス幅がでかいと、かなり長期間にわたってバーナキ議長は利上げ出来そうにない、ということになる。アメリカは金融政策の出口戦略とか議論する段階からは程遠いね、ということになるが、この点で、よく衝突する二人の意見は一致しているようだ。

Krugmanが言う

my sense is that a lot of people just can’t bring themselves to face
the reality that we’re likely to be in a zero-interest world for a long
time. They just keep assuming that the Fed is going to raise rates
soon, even though there is absolutely nothing about the macro situation
that would justify such a rate increase.

But once again: if you take standard economic forecasts seriously,
they point to near-zero short-term rates for a very long time, which in
turn justifies low longer-term rates.

という意見は正しいと僕も思うし、Mankiwも

Nonetheless, I think Paul and I agree that this equation provides
a reasonable first approximation to what the Fed will and should do in
response to macroeconomic conditions.

と同意している。というか、そろそろFRBは利上げするでしょ、って誰が言いだしっぺ？

話はそれるけど、いろいろ複雑なtaylor ruleがある中で、こういう単純な線形モデルを「a reasonable first approximation」ということで気軽に使って議論するのって、なかなかお手軽でいいっすね。

調子に乗って日本のデータをつかってmankiw ruleをいろいろと推定してみた。ちょっと、いくつか注意点を。

注意点

１）政策金利としてコールレートを使った場合は、（金利が自由化された）1994/10以降のデータを使ってみた。いまググってみつけた日銀レビューのこういうペーパーとかを見たら、1994年をまたいで普通にコールレートデータを政策金利として分析しているようだ。
２）公定歩合データを使って1988-2008の期間で推定するのに、何の意味があるのか自分でもよくわからないが、とりあえずやってみたよ、という感じ。でも、なんか当てはまりはやたらいいんだよなー。
３）ｔ値はほぼ有意だった。あ、エクセルの分析ツールつかったお手軽分析なので、whiteの頑健な一致推定量を使うとかそんなところまで出来てません。
４）いかにもガウスマルコフの古典的仮定が崩れてそうな匂いがプンプンするけど、遊びなのできにしない。
５）アメリカでcore cpiと呼ばれているもののjapanese dataのcounterpartは、コアコアCPIを呼ばれているもの。ややこしいね。食糧とエネルギーを除いた物価変動。

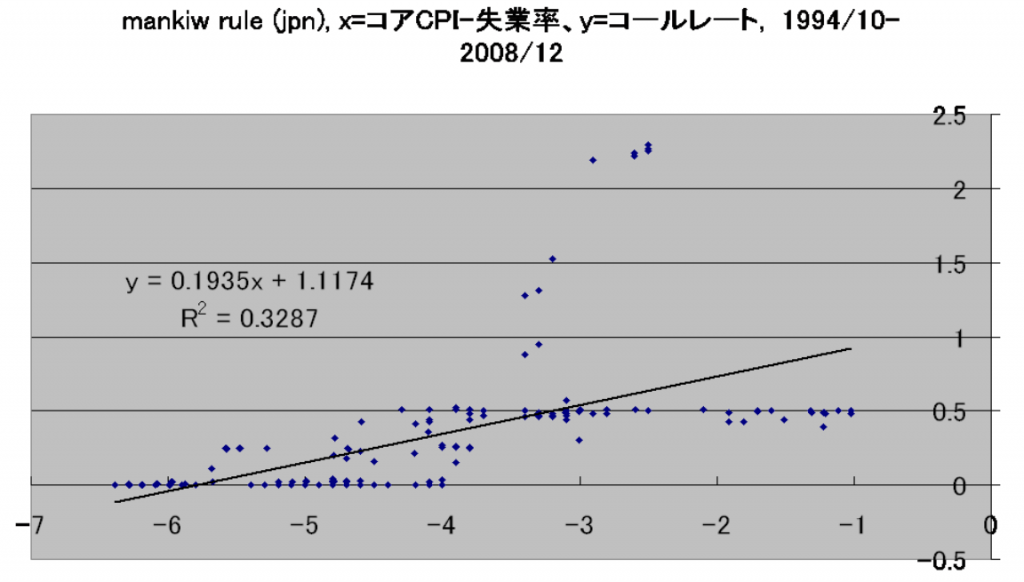
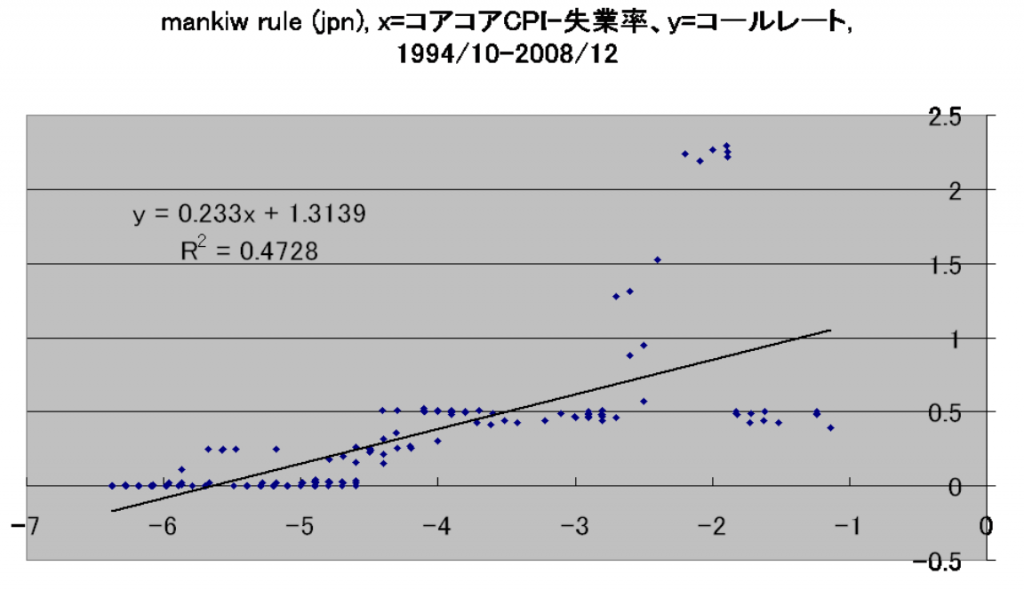
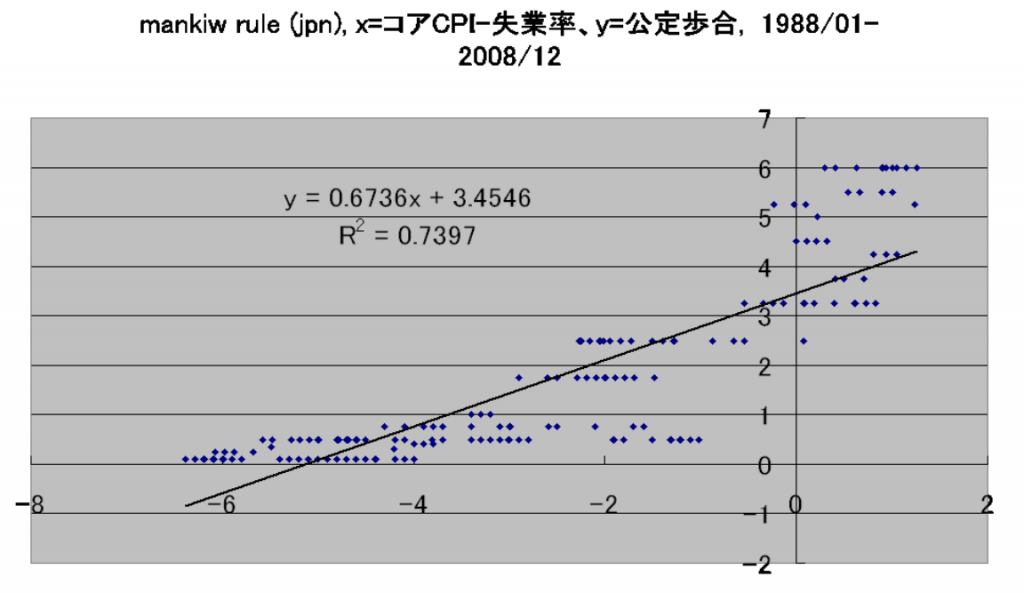
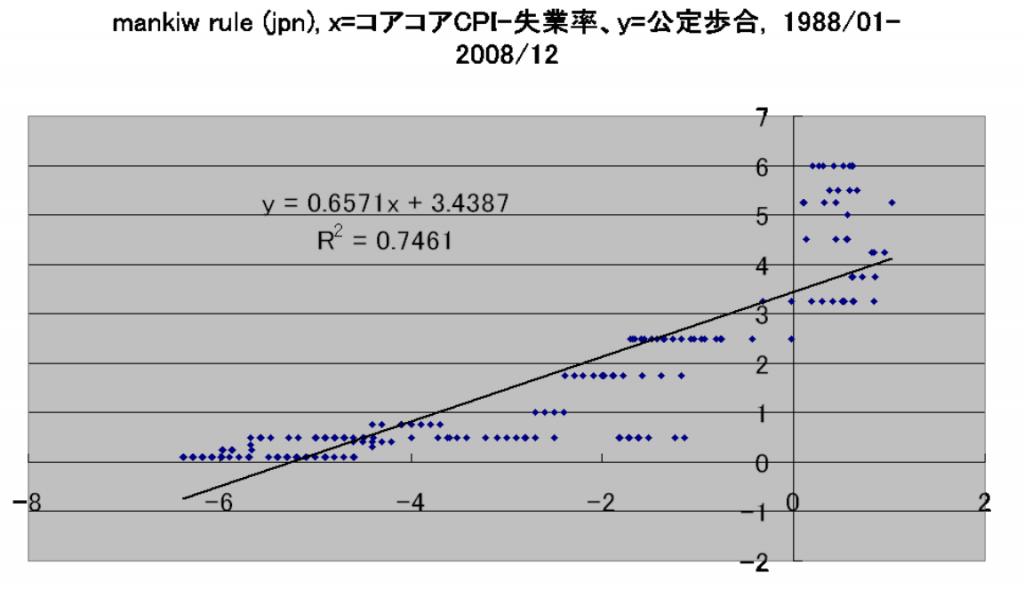
考察をいくつか。

１．どの推定結果を使っても、現状では政策金利がゼロ以下の理論値になる。上から順番に、それぞれ-0.100775747, -0.275370937, -0.100775747, -0.275370937になる。
２．どの推定結果を使っても、2006年3月の量的緩和解除する前、かなり長い期間、政策金利の理論値はプラスだった。一番短かったもので、2004年10月にはプラスに転じていた（4番目のグラフ）。出来れば利上げしたくてたまらない、という感じのじれったい期間を経て、2006年3月にようやく量的緩和を解除、7月にはゼロ金利も解除した、という気持ちが読み取れる。当時、時期尚早だろうという議論もあったが、日銀としてはかなり我慢した後の利上げだったのが分かる。
３．2000年8月のゼロ金利解除の翌月に、4グラフのうち、1つでもうマイナスの政策金利の理論値を出しているものがある（3つ目）。2001年3月の量的緩和に踏み切る頃には、4つのうち3つで、政策金利の理論値がマイナスになっていた。やはり、あのゼロ金利解除は失策か。
４．上述した通り、アメリカでは政策金利の理論値が-6.4。それに比べたら、日本は随分出口に近いと言えるのか？
５．「FRBのほうが早く利上げするだろう」説の元締めは一体誰？mankiw ruleで政策金利が0になる条件は、x=5.1。これを満たすcore inflationとunemployment rateの組み合わせは、 (0%, 5.1%), (1%,6.1%), (2%, 7.1%)とかだが。どれも実現しそうにない。現状の失業率は9.5%もあるし、これが年内に6~7%まで落ちるとは思えない。年内のFRB利上げは、たぶん無い。
６．「FRBのほうが早く利上げするだろう」説は、「年内にFRBが利上げするだろう、でも日銀はできないだろう、だから今年の後半は円安圧力があるんですよ」という説に発展していた。「「年内にFRBが利上げ」観測はどこの誰が流したのか知らないが、現時点で普通に考えたら、そんなことはもう起きない。
７．日本はデフレに苦しんでいるけれど、アメリカは失業率が高すぎて苦しんでいる。むしろ、FRBと日銀でより困っているのはFRBのほうかもしれない。
８．異常だと思っていた現在の円高も、こう考えると自然な現象かもしれない。「日銀も大変だけど、FRBのほうが利上げにこぎつけるのは大変そうだ。」ということになれば、ドル買うメリットは薄いし、しかも日本はデフレ国家だからその通貨は、円高になる、という理屈。
９．現実経済に関するコメントなんて、いくらでも理屈を作れるので、ここに書いてあることを読んで、なるほどー、とか思ったらダメダメー。

ちょっと書こうと思っただけなのに、かなり時間がかかって長いエントリーになってしまった・・・・さ、寝よ。

（追記）
いま思い出したけど、Krugmanは出口戦略が時期尚早だ、と、去年の9月にも言っている。

金融政策の出口戦略について

（追記２）
推定結果について、その後ちょっとだけ調べてみた。係数は上記の通り。分散不均一性ありそうだけど、white修正してもt値は有意のままなので問題無し。系列相関は・・・うわ、やはりかなりありそうで、ちょっとこれは深刻な問題を引き起こしているかもしれない。重要変数のomitが原因ならばサヨナラ一致性（定数項と係数の両方とも）になるし、関数形の特定化エラーなら、それもそれで深刻な問題だ・・・。あと疑問に思っているのが、名目金利はマイナスにならないのに、非負制約を課すようなモデル（半対数法とか）を使わなくっていいのかな、という点。現実にはマイナスにしないだけで、数学的には可能だからOKなのだろうか？半対数法は試してみたけど、そんなに推定結果のパフォーマンスは向上しなかったし。